記事の内容
今回の記事は、プログラミングの問題としてはそこそこ有名な「Nクイーン問題」をPythonで解いてみます。
「問題解決のpythonプログラミング 数学パズルで鍛えるアルゴリズム思考法」という本からの引用になります。本書は、pythonを用いて基礎的な知識だけで数学パズルを解く楽しさを教えてくれる本です。アルゴリズムのいい練習になります。
それでは、解答をまとめていきます!!
問題解決のPythonプログラミング 「女王たちを一緒にするな」
Nクイーン問題の具体例として、8クイーン問題を扱います。
8クイーン問題では、8×8マスのチェス盤において、8つのクイーンをどのクイーンにも取られないように配置するにはどうすればいいのかという問題です。 クイーンの動き方は、次の写真のように縦横斜め全部です。
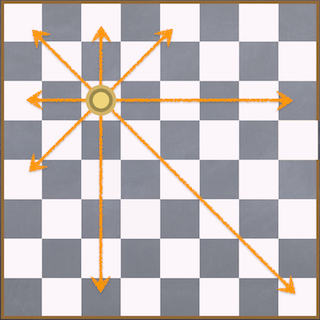
この問題を解くための条件は3つあります。
1、どの2つのクイーンも同じ列にない
2、どの2つのクイーンも同じ行にない
3、どの2つのクイーンも対角線方向の線上にいない
どう工夫するか?
マス目を2次元リストで表現したくなるのは、自然な思考。
しかし、条件を考えれば、インデックスが列を表し、値がクイーンのある行を表す1次元配列で済ませることができる。
例えば、[-1, 2, 0, 3]ならば、-1は列にクイーン無し、0はその列の1行目、3はその列の4行目にクイーンがあることを表す。
この表現方法ならば、そもそも同じ列に2つのクイーンを置くことができない。第一規則はチェックしなくていい!!!
解答
def noConflicts(board, current): for i in range(current): if ( board[i] == board[current]): #これまでの列に同じ値がないかチェック return False if (current - i == abs(board[current] - board[i])): #対角線方向のこのチェックは工夫あり。インデックスと値が等しくなるという性質を利用。絶対値に注意。 return False return True #continue文を使うことで、その下の実行は全てスキップされる def EightQueens(n=8): board = [-1] * n #空の盤面の作成 for i in range(n): board[0] = i for j in range(n): board[1] = j if not noConflicts(board, 1): continue for k in range(n): board[2] = k if not noConflicts(board, 2): continue for l in range(n): board[3] = l if not noConflicts(board, 3): continue for m in range(n): board[4] =m if not noConflicts(board, 4): continue for o in range(n): board[5] = o if not noConflicts(board, 5): continue for p in range(n): board[6] = p if not noConflicts(board, 6): continue for q in range(n): board[7] = q if noConflicts(board, 7): print(board) return
もっと綺麗に解けるか
今回のコードは、力任せにループで解いている。コードとしては、やや汚い。本書によると、再帰的な手法でもっと綺麗に書けるらしい。今後、本書を読み進めることで改めて挑戦してみたい。
本書に興味が湧いた人はぜひ手にとってみてほしい。





